Efficient construction of linear models in materials modeling and applications to force constant expansions

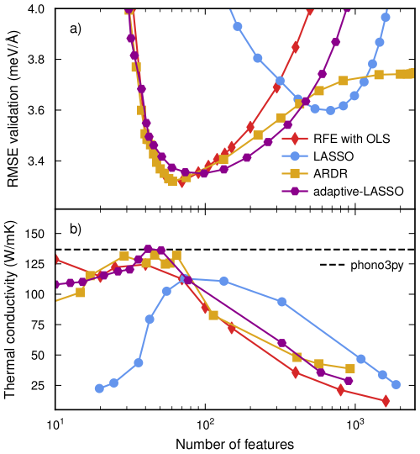
Linear models, such as force constant (FC) and cluster expansions, play a key role in physics and materials science. While they can in principle be parametrized using regression and feature selection approaches, the convergence behavior of these techniques, in particular with respect to thermodynamic properties is not well understood. Here, we therefore analyze the efficacy and efficiency of several state-of-the-art regression and feature selection methods, in particular in the context of FC extraction and the prediction of different thermodynamic properties. Generic feature selection algorithms such as recursive feature elimination with ordinary least-squares (OLS), automatic relevance determination regression, and the adaptive least absolute shrinkage and selection operator can yield physically sound models for systems with a modest number of degrees of freedom. For large unit cells with low symmetry and/or high-order expansions they come, however, with a non-negligible computational cost that can be more than two orders of magnitude higher than that of OLS. In such cases, OLS with cutoff selection provides a viable route as demonstrated here for both second-order FCs in large low-symmetry unit cells and high-order FCs in low-symmetry systems. While regression techniques are thus very powerful, they require well-tuned protocols. Here, the present work establishes guidelines for the design of protocols that are readily usable, e.g., in high-throughput and materials discovery schemes. Since the underlying algorithms are not specific to FC construction, the general conclusions drawn here also have a bearing on the construction of other linear models in physics and materials science.

Associated data

Data and code (via gitlab)