Variational polaron self-interaction-corrected total-energy functional for charge excitations in insulators

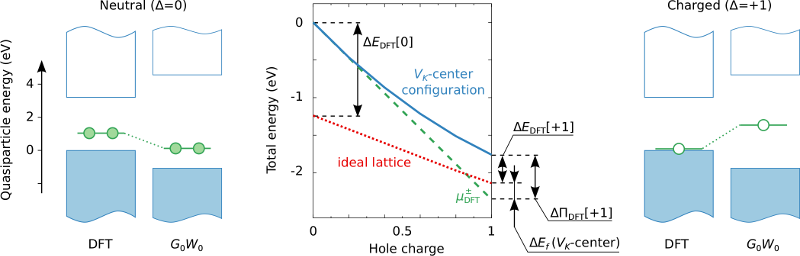
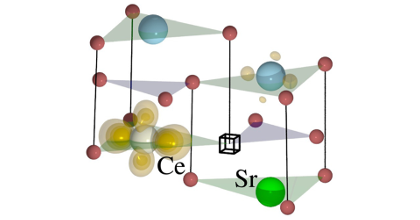
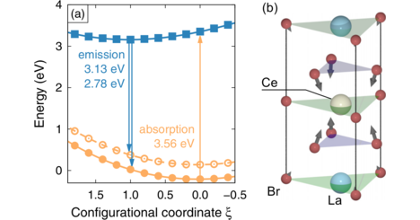
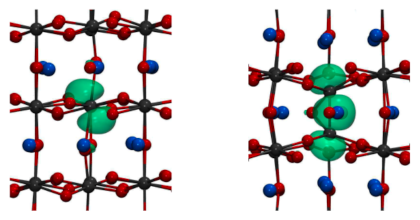
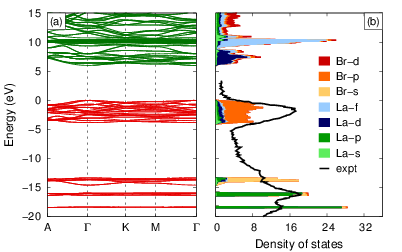
We conduct a detailed investigation of the polaron self-interaction (pSI) error in standard approximations to the exchange-correlation (XC) functional within density-functional theory (DFT). The pSI leads to delocalization error in the polaron wave function and energy, as calculated from the Kohn-Sham (KS) potential in the native charge state of the polaron. This constitutes the origin of the systematic failure of DFT to describe the polaron formation in band insulators. It is shown that the delocalization error in these systems is, however, largely absent in the KS potential of the closed-shell neutral charge state. This leads to a modification of the DFT total-energy functional that corrects the pSI in the XC functional. The resulting pSIC-DFT method constitutes an accurate parameter-free ab initio methodology for calculating polaron properties in insulators at a computational cost that is orders of magnitude smaller than hybrid XC functionals. Unlike approaches that rely on parametrized localized potentials such as DFT+U, the pSIC-DFT method properly captures both site and bond-centered polaron configurations. This is demonstrated by studying formation and migration of self-trapped holes in alkali halides (bond-centered) as well as self-trapped electrons in an elpasolite compound (site-centered). The pSIC-DFT approach consistently reproduces the results obtained by hybrid XC functionals parametrized by DFT+G₀W₀ calculations. Finally, we generalize the pSIC approach to hybrid functionals, and show that in stark contrast to conventional hybrid calculations of polaron energies, the pSIC-hybrid method is insensitive to the parametrization of the hybrid XC functional. On this basis, we further rationalize the success of the pSIC-DFT approach.