Quantitative predictions of the thermal conductivity in transition metal dichalcogenides: Impact of point defects in MoS2 and WS2 monolayers

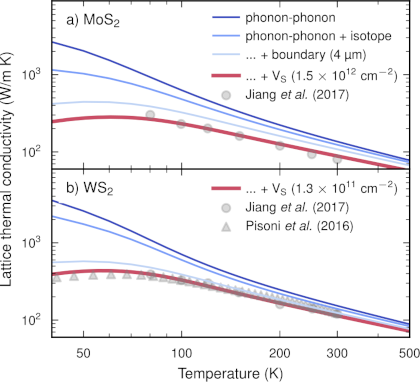
Transition metal dichalcogenides are investigated for various applications at the nanoscale because of their unique combination of properties and dimensionality. For many of the anticipated applications, heat conduction plays an important role. At the same time, these materials often contain relatively large amounts of point defects. Here, we provide a systematic analysis of the impact of intrinsic and selected extrinsic defects on the lattice thermal conductivity of MoS₂ and WS₂ monolayers. We combine Boltzmann transport theory and the Green’ s function-based T-matrix approach for the calculation of scattering rates. The force constants for the defect configurations are obtained from density functional theory calculations via a regression approach, which allows us to sample a rather large number of defects at a moderate computational cost and to systematically enforce both the translational and rotational acoustic sum rules. The calculated lattice thermal conductivity is in quantitative agreement with the experimental data for heat transport and defect concentrations for both MoS₂ and WS₂. Crucially, this demonstrates that the strong deviation from a 1/T-temperature dependence of the lattice thermal conductivity observed experimentally, can be fully explained by the presence of point defects. We furthermore predict the scattering strengths of the intrinsic defects to decrease in the sequence V_Mo ≈ V_2S⁼ > V_2S^⊥ > V_S > S_ad in both materials, while the scattering rates for the extrinsic (adatom) defects decrease with increasing mass such that Li_ad > Na_ad > K_ad. Compared with earlier work, we find that both intrinsic and extrinsic adatoms are relatively weak scatterers. We attribute this difference to the treatment of the translational and rotational acoustic sum rules, which if not enforced can lead to spurious contributions in the zero-frequency limit.