Investigating the missing-wedge problem in small-angle X-ray scattering tensor tomography across real and reciprocal space

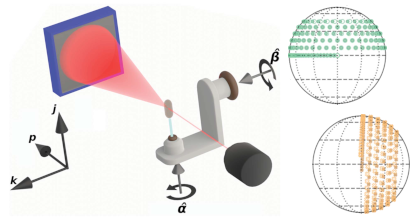
Small-angle scattering tensor tomography is a technique for studying anisotropic nanostructures of millimeter-sized samples in a volume-resolved manner. It requires the acquisition of data through repeated tomographic rotations about an axis which is subjected to a series of tilts. The tilt that can be achieved with a typical setup is geometrically constrained, which leads to limits in the set of directions from which the different parts of the reciprocal space map can be probed. Here, we characterize the impact of this limitation on reconstructions in terms of the missing wedge problem of tomography, by treating the problem of tensor tomography as the reconstruction of a three-dimensional field of functions on the unit sphere, represented by a grid of Gaussian radial basis functions. We then devise an acquisition scheme to obtain complete data by remounting the sample, which we apply to a sample of human trabecular bone. Performing tensor tomographic reconstructions of limited data sets as well as the complete data set, we further investigate and validate the missing wedge understanding of data incompleteness by investigating reconstruction errors due to data incompleteness across both real and reciprocal space. Finally, we carry out an analysis of orientations and derived scalar quantities, to quantify the impact of this missing wedge problem on a typical tensor tomographic analysis. We conclude that the effects of data incompleteness are consistent with the predicted impact of the missing wedge problem, and that the impact on tensor tomographic analysis is appreciable but limited, especially if precautions are taken. In particular, there is only limited impact on the means and relative anisotropies of the reconstructed reciprocal space maps.

Associated data

mumott homepage
mumott on gitlab
mumott releases (zenodo)